Problem Set 2.
Problem 2.1
Corresponding to Lecture 2
This Pset was done in with my clasmates Erik Strand, Alex Berke and Eyal Perry.
The way we did this 4 folded elements was the following. We started thinking algorithmically if we could say without folding if there was any condition that told us that the crease patters were or not flat foldable. Then we got tired by seeing that that was tricky and did not warantee that it was flat foldeble, so we started directly folding (maybe it was not the best decision but led us to a great lesson!). We started folding the symmetric guy, that was suggesting us that clearly was flat foldable.
And it was!
So we got hyped and decided to do the crease pattern a. Again, it was flt foldable to we felt confident. Then b came and I thought I folded it! But when unfolded it we realize we did extra creases.
Lesson Learnts came here
We realized how we needed to analyze a little bit more the patterns before fold them. Clearly here there were a node that was not satisfying Kawasaki! Find attached here all the images folded or in case that doesnt fold, the analysis why is not flat foldable.
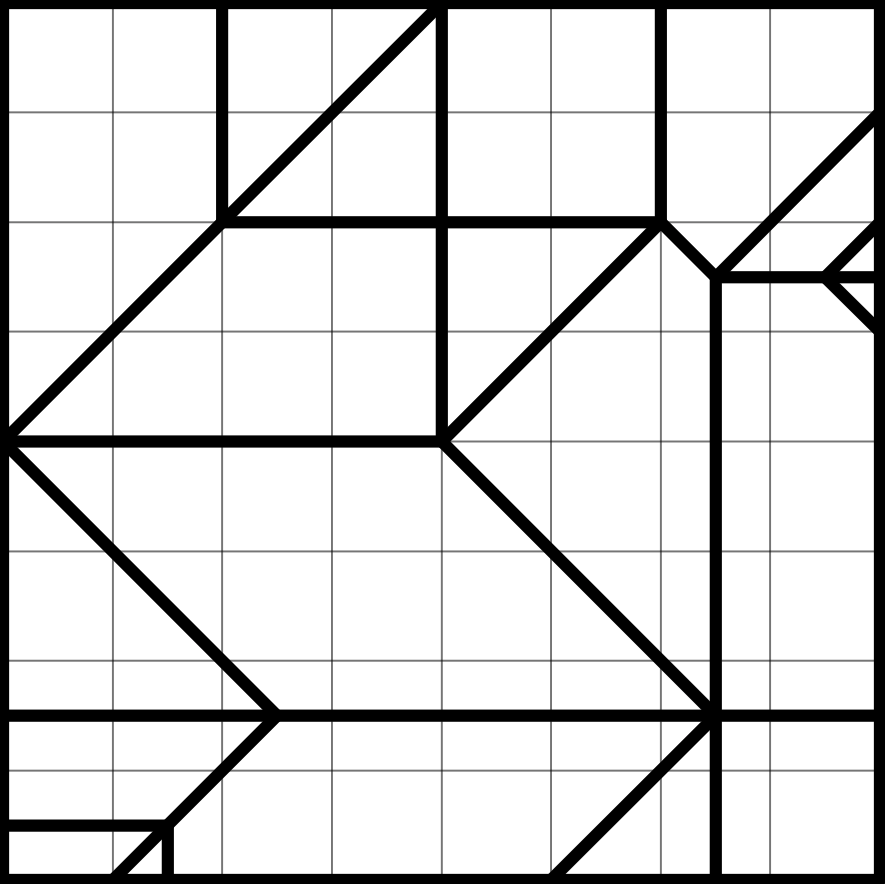
Crease Pattern A
This pattern was the second we did and it folded nicely. The last fold was very exciting.Crease Pattern B
So we thought it was flat foldable... But nope.
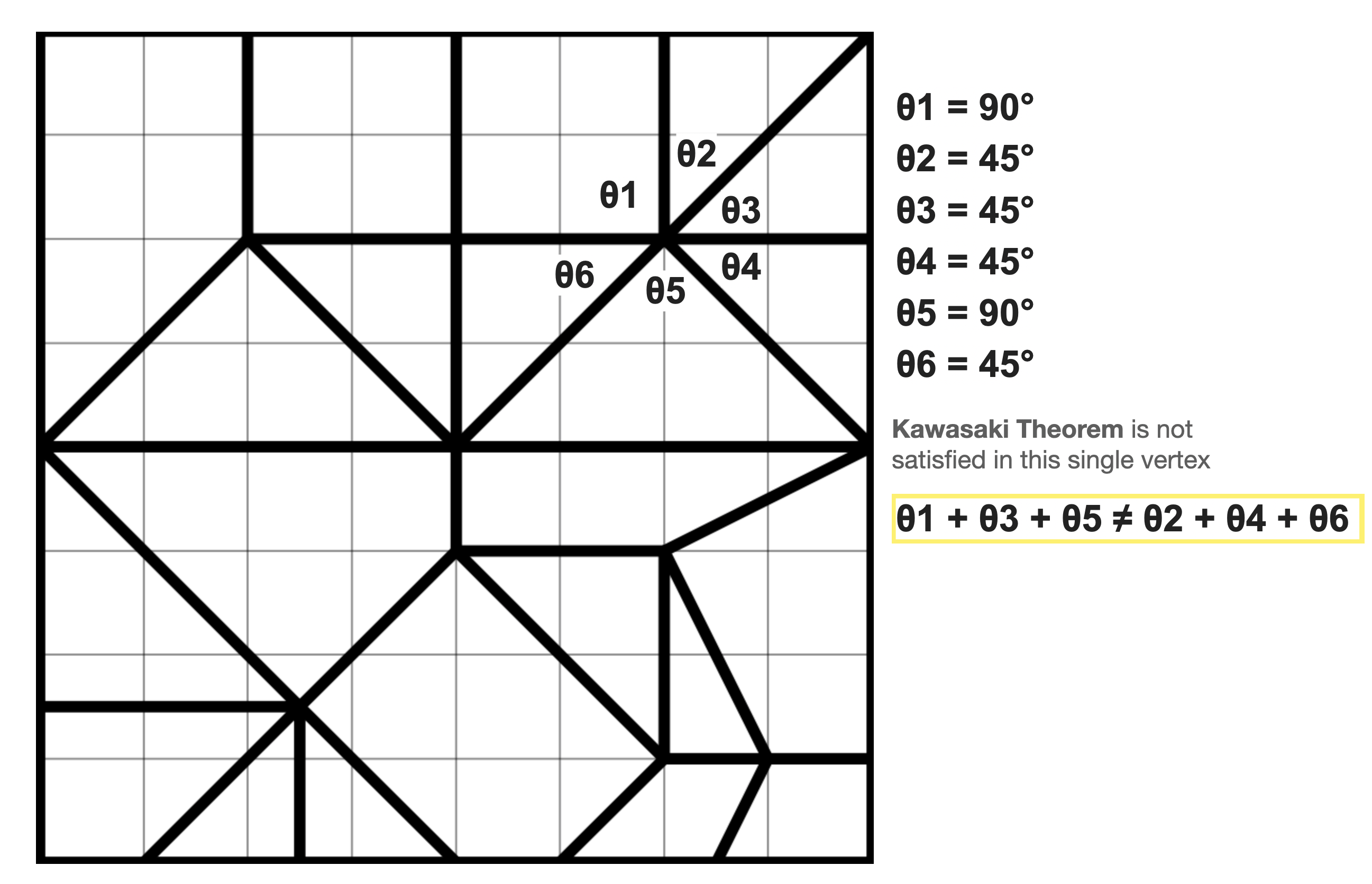
After unflding it we saw we made (IN THE LAST STEP) extra crease patterns. After analyze it we saw that Kawasaky theorem was being not accomplished in the following node
Crease Pattern C
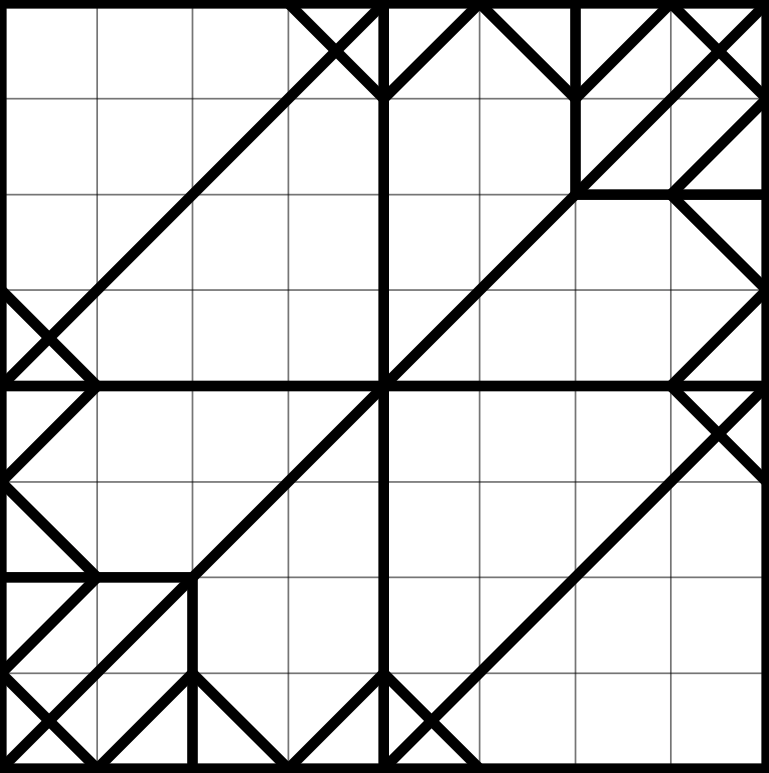
This crease pattern was the first we did due to the beautiful symmetry it was suggesting us. It was flat foldable.Crease Pattern D
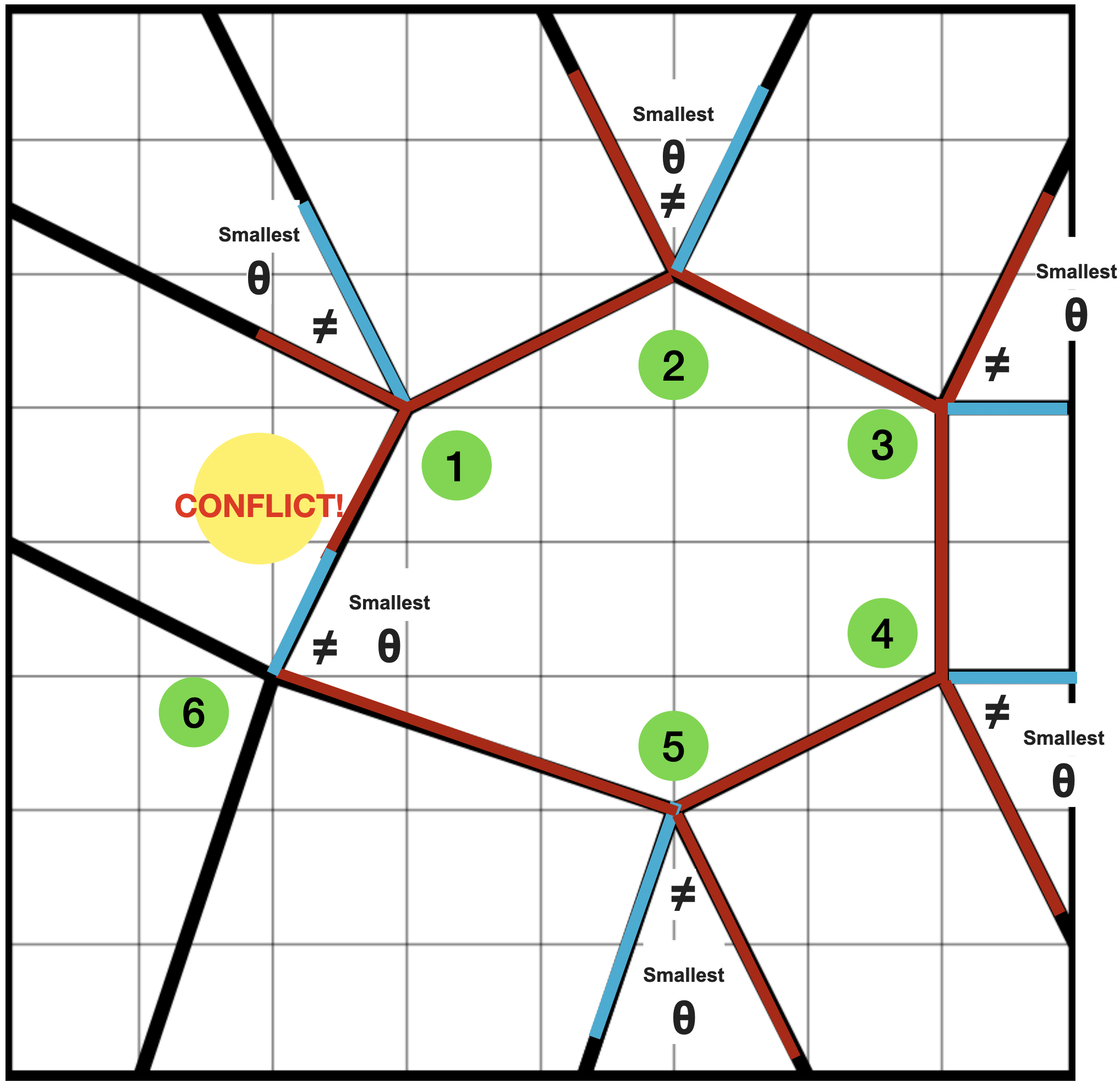
This was a beautiful case. We concluded that it was not foldable without doing a single fold. The image illustrate how we did concluded the solution. Looking at the inner polygon, there is always a smaller angle in every vertex. That means that MUST be mingling, meaning each crease that defines the angle can not be equal ( MM or VV is not allowed. Must be MV or VM ). So, if we start in an arbitrary vertex, called one, we can impose a virtual MV assignment for the smaller angle of this vertex. Because of Maekawa Theorem, there is only one solution possible in each node ( MMMV or VVVM ). Looping thorugh all the vertex of the poligon (one vertex of the node 1 will impose some order in the node 2) we arrive to the same place we started suggesting a different sign!This is a clear statement that is not foldable!
Problem 2.2
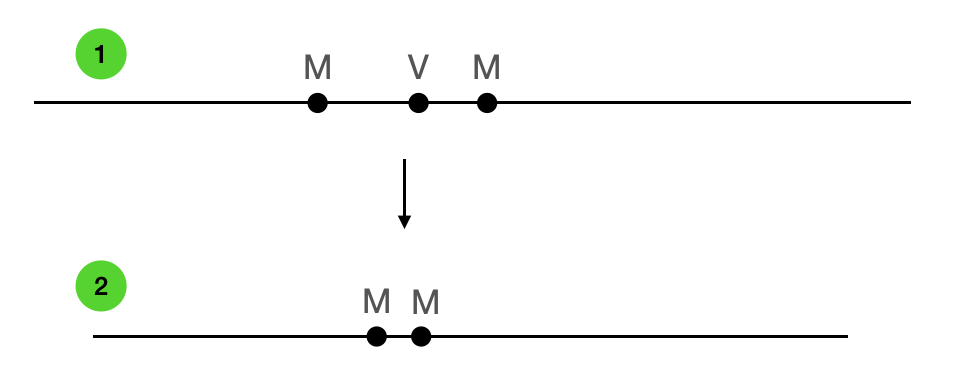
a) Draw a 1D crease pattern that is mingling but not flat foldable.
As far as I understand mingling, it implies that patterns 'minglability' in every state can be different. Mingle is a condition that ensure you to give the next step but doest not guarantee that the rest will be flat foldable. It preserves flat foldability (if it already exist in the pattern) for but not warrantee it. As an example of a 1D crease able to mingle (in the state 1) but cant be flat foldable (state 2) is shown bellow:b) Draw a folded state including stacking of a 1D pattern that cannot be achieved by crimps and end folds.
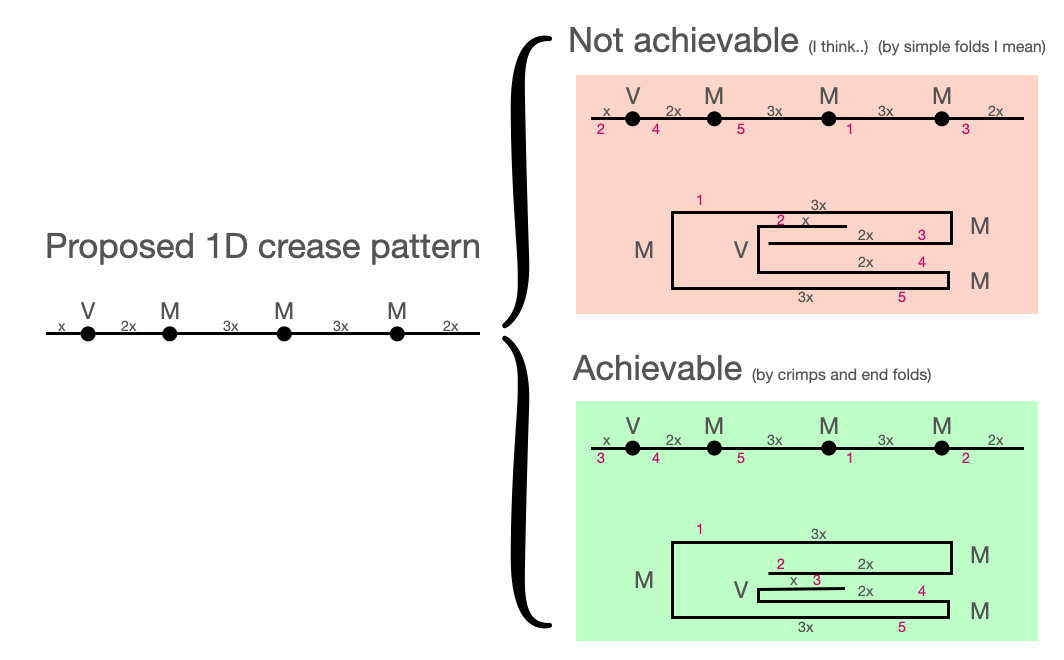
It took me a while to fully understand end fold and how will be called other folds (like just a flat fold in the midle node). So far, what I have understood is that the key of this question resides in the stacking order, meaning that I am going to propose a crease pattern with a MV assignment that can not achieved a proposed stacking with single folds . On the other hand, the proposed crease pattern is flat foldable and will be able to reach other possible stackings.
back to menu