Problem Set 1.
Corresponding to Lectures 1 and 2
Problem 1
The problem I will describe is the reason of me joining to this class. My approach to Origami has been from an engineering perspective but I want to develop skills to solve this problem algorithmically to provide a tool that generate the desired Ms Vs pattern.
For my master thesis, I am interesten on research discrete cellular soft robotics. One of the points to study is the skining of a discrete lattice structure. Because the size of the lattice is a fixed octahedron, achieving shapes with curvature is not possible.
For this reason, I want to provide a folded structure that will live between the voxel and the outer shape (green zone), that will be the responsible of ensuring the final outer shape and provide mechanical stability to it.
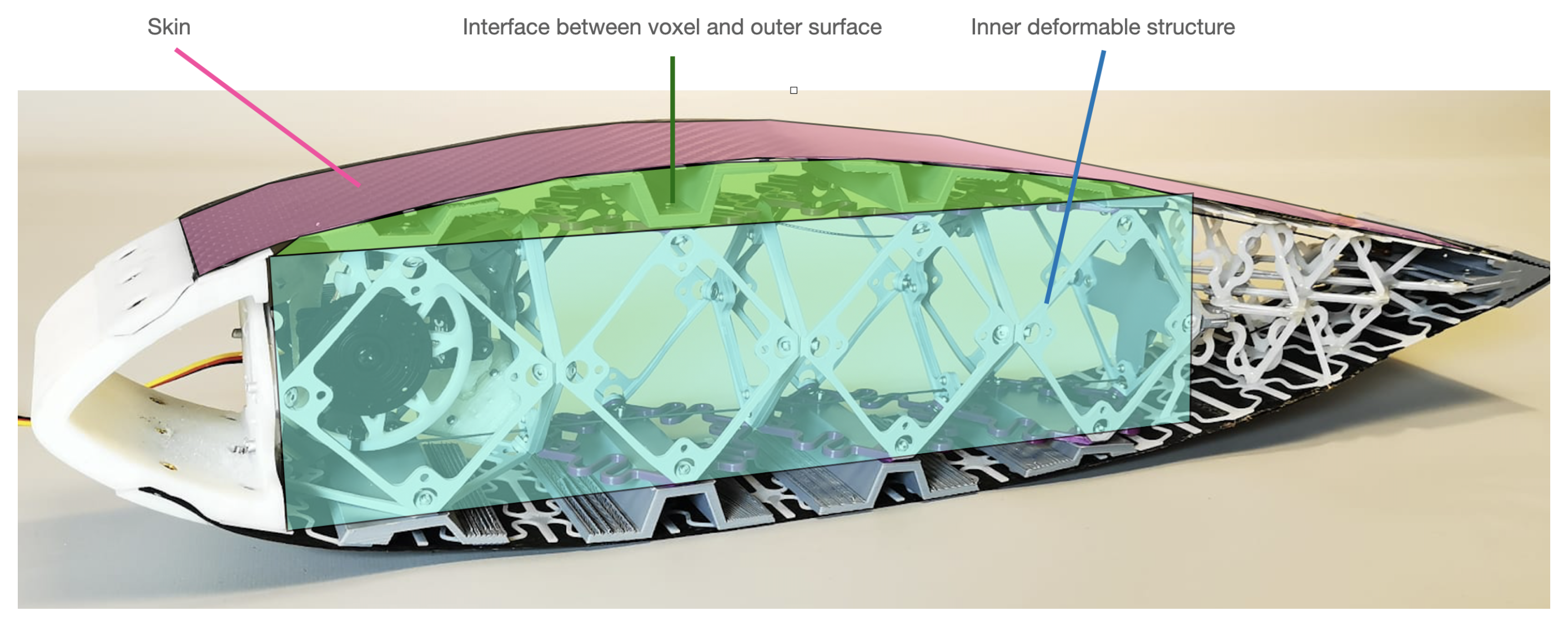
I am interested on filling two arbitrary surfaces with folds. But there are some constrains that makes the desired sollution a little bit specific. The lower surface is a flat surface
Some candidate I am highly interedted is a miura ori tessellation but with the following modifications:


One great point that I would love to introduce as a restriction is to respect the footprint of the rivet faces of the voxels to rivet the fold with the structure and provide the final shape, as it can be seen in the green structure (I know this specific form is not rigid origami foldable)
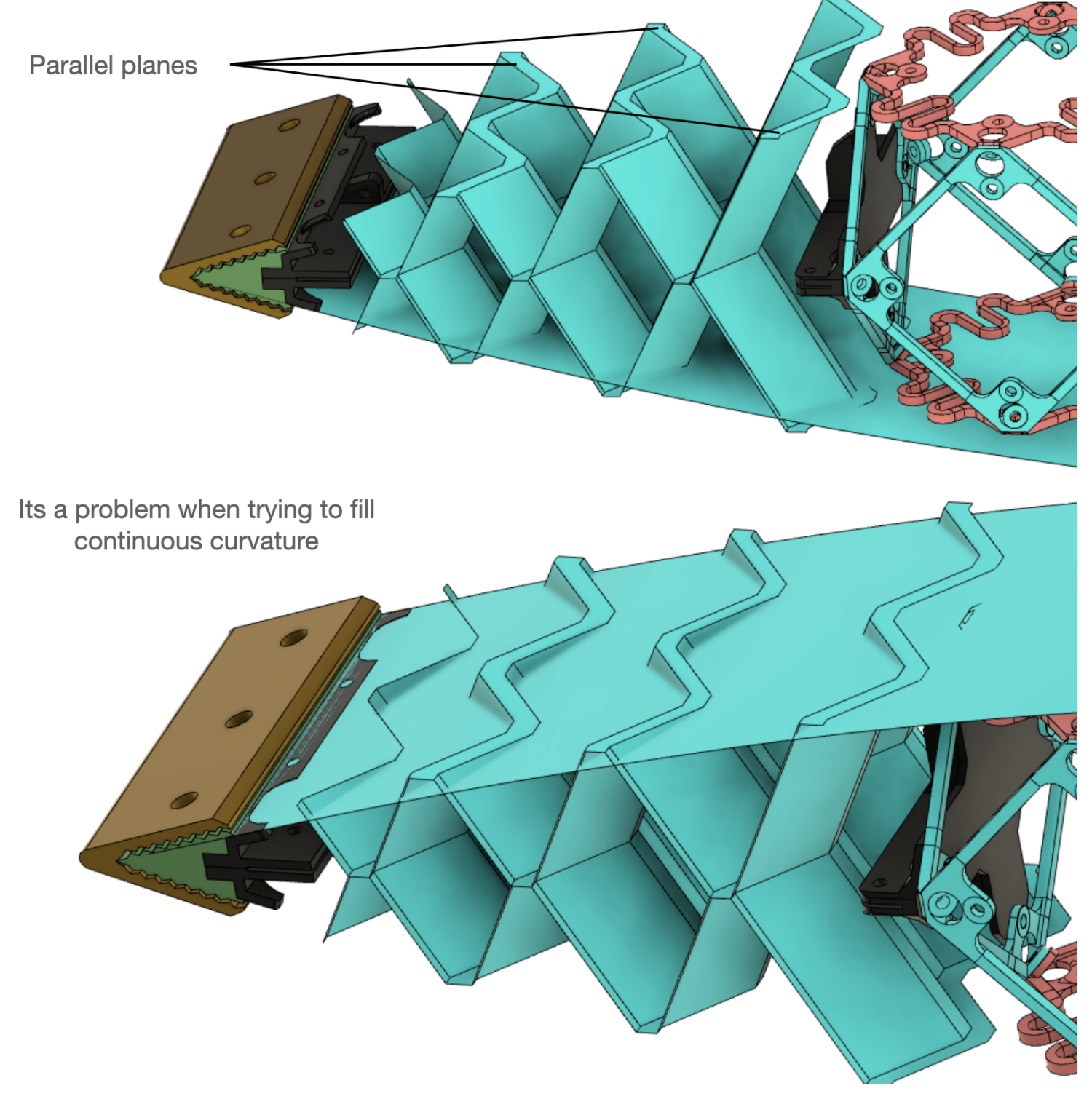
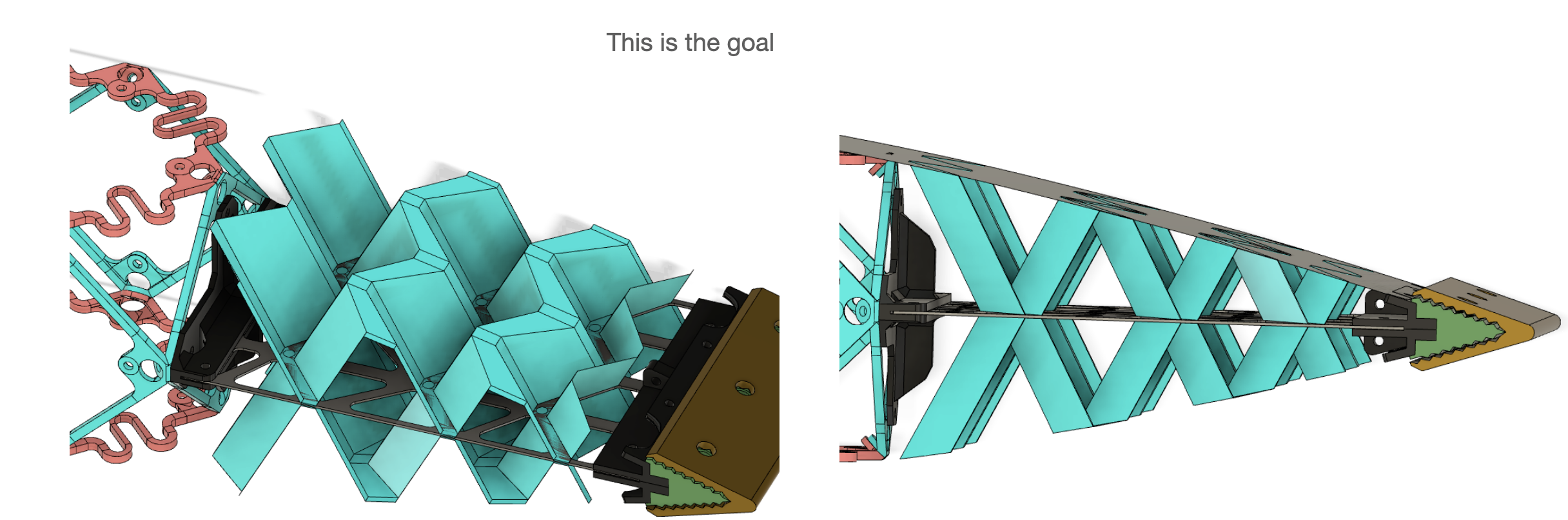
So the question will be. First, find an available modificaiton of the miura ori that allows to have chamfers and then, find an algorithm that computes the mountains and valleys of the volume to fill (ideally 2 curvature on the top but will start with 1 curvature) that respect the rivets footprint in the lower flat surface.
Problem 2
I have been able to make 2/3 of the puzzles. The T shape one was challenging




Problem 3
Ive been able to make only the first part!



