HW3. Python and Grasshopper. Build your own FDM and lets play .

Files to download

Assignment

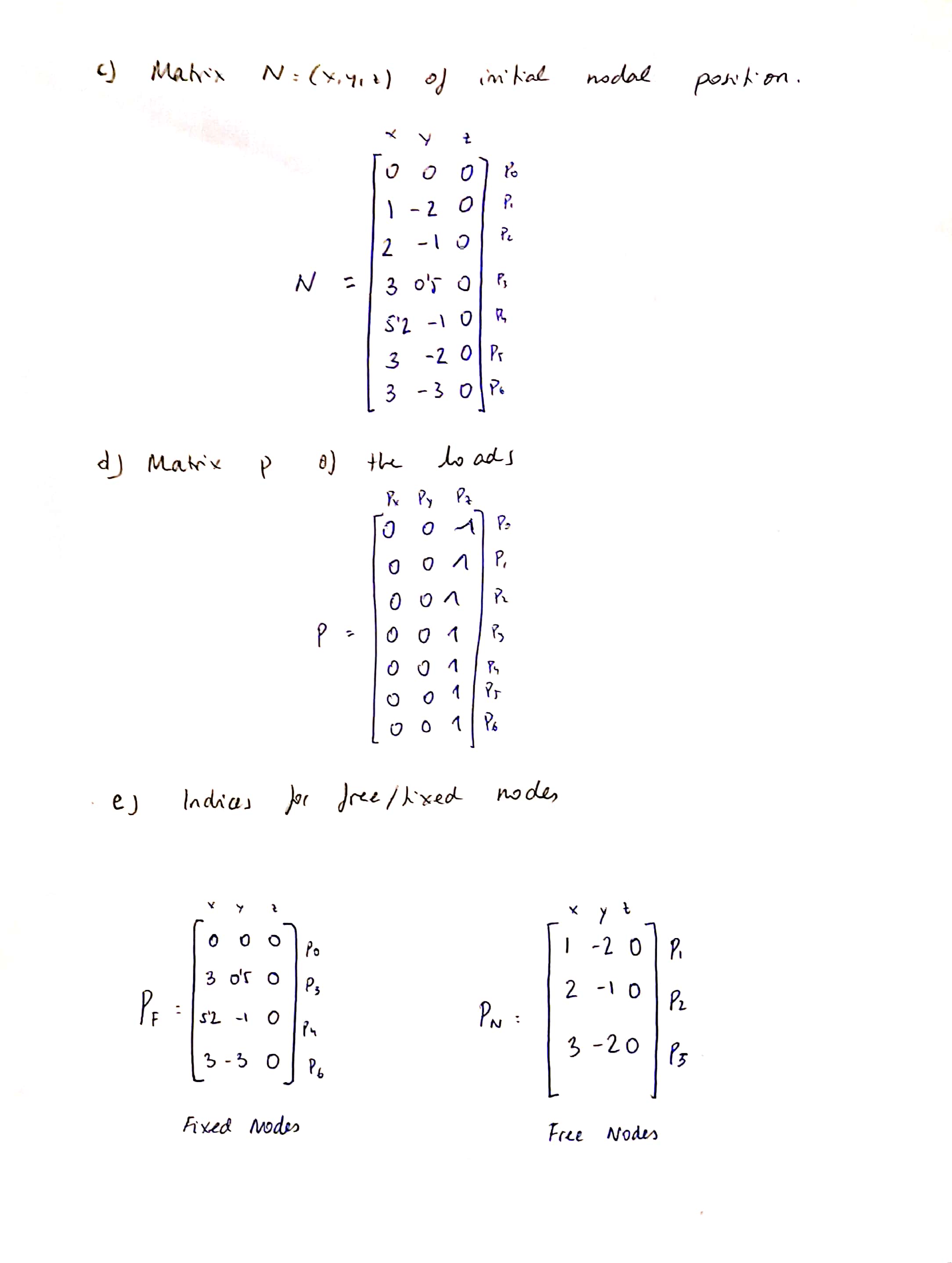
a_ Force Density Method

This first part of the assignment is crutial. Consist on reading the proposed paper by Linkwitz and be able to first, solve a simple 4 fixed point 1 free node problem. This solution can be done without matrix aproximation so analitically has got a straight forward sollution.

Please, find attached the scanned papers I made to solve manually those equations for part A.

b_ Computational FDM

Once we have readed and internalized the paper, undertood the equations aswell as the linear matrix eqution sistem to be solved by Numpy, it is time to start coding in python to be able to firstly, plot the solver in the internal python graphs, and secondly, link this script to grasshopper to be able not only to visualize it better, but to interact with it! This is the huge potential of grasshopper. It is a great friendly User Interface but also it is a parameter playground in which manually and by code we can modify those parameters. This is the perfect scenario to be appied then, some optimization methods or FEM or any analysis we want to do!

Once the code has been done and it has been prove that it works, the output chart python gives you is the following:

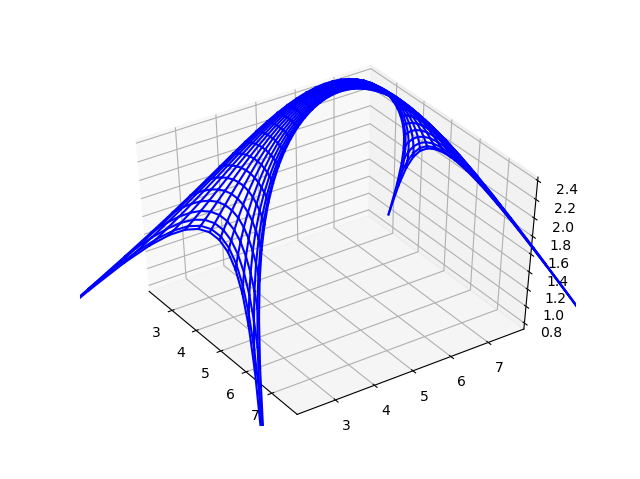
The code written to do this is the following:

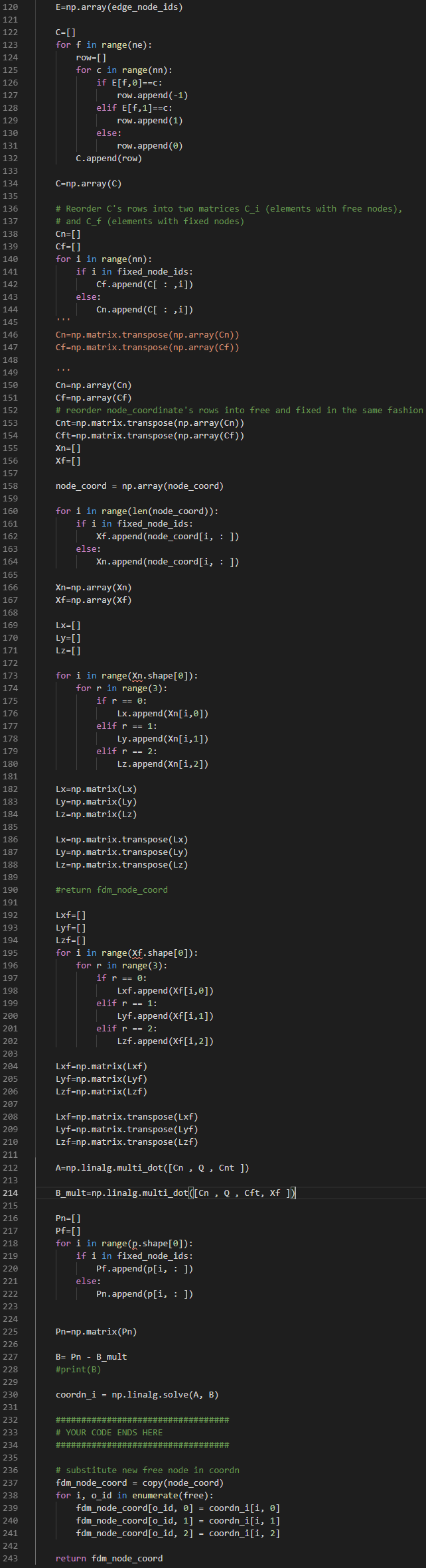
Also this full script can be found in the attached documents.

We can jump directly to the third point of the b section. The one that tells you to compute 12 geometries playing with the grasshopper user interface, using as a background solver the code we have written! Once I achieved (not without suffering) the proposed task, those are the 12 structured I plotted.

The forth and fith part of this b section is asking for introdude any FEM solver in our grasshopper structure and start iterating with a selected geometries inside the design space we consider interesting. To do that, to complete the forth point, I had defined a certain geometry (15mx15m area) and I am going to start modifying the number of bars to see how it affects to our volumetric standard. Here it can be found the data iterated and the plot tendency

Plot discussion

As it can be seen, the tendency of the volume is showing an exponential growth. To the same area ( 15m x 15m) to a constant load in each node, we are finding that anincrement in the number of bars affect to the square to the force per length. The nature of the increment of bars is also exponential due to we are increasing this numner in the x and y axis, generating more nodes in an exponential way. If each of this node will have assigned a constant force, it makes sense that, inside the formula F x L, L is the one that set the order of magnitude of this growing.

The fith point is inviting us to increase one more variable to this plot, to be able to work with two parameters as Design Space Drivers. I have added the area in this case. To a same number of bars, I am going to plot areas with values of 1m2, 25m2, 100m2 225m2 and 400m2 (In the plot I will refer only to one side, so the axis will be marked as 1m,5m,10m,15m,20m). to this area values I will plot geometries formed by shells composed by a square array of 4,5,6,7,8,9, and 12 lateral sides of the initial flat grid. The result of this experiment is the following design space

c_ Computational Dynamic Method

I have choosen the easyest first structure I plotted when connected python and grasshopper to try to find the form of this shape using other form-finding tool. To do that, I baked the desired form to find and changed the gh script to see which parameters in Kangoroo2 should I touch to reproduce it. I realized that Kangaroo solves the goal structure based in the grid, in some parameter that modifies the length and some other that modifies the force. But the bars looks so relaxed, is more like solving a geometrical problem rather than a equilibrium of forces problem. Playing with the force and the length values, I didnt achieve an exact form (because it dont solve using the fdm method the shape will never be the same) but this is the image of the most similar looking shape I found.

The main difference I can saw was that FDM solve a length of the bars based in the surrounding conditions and force density of the bars. but the initial length of all bars are the same. The thing I saw in Kangaroo is that an input of a desired lenght is given and it will modify the final shape of the grid. Is like transform the planar grid to a courved grid giving the increment that each bar will have and a force that will take them to this shape. In other words, I see that the resultant grometry in Kangaroo has got a more homogeneus load distribution than the FDM structure based on that almos each bar has the same length.

back to menu